
 236 usuarios conectados
236 usuarios conectados
/natureduca/fisica-movimiento-los-movimientos-rectilineos-01

Física
EL ESTUDIO DE LOS MOVIMIENTOS
Los movimientos rectilíneos - 1ª parte
Introducción
 os movimientos rectilíneos constituyen un tipo particular de
movimientos cuyo estudio presenta un especial interés. En primer lugar, son los
movimientos más sencillos, de modo que su comprensión permite una generalización
posterior a situaciones más complejas. Estos movimientos más complicados pueden
ser estudiados como la composición de movimientos rectilíneos elementales. Tal
es el caso, por ejemplo, de los movimientos de proyectiles.
os movimientos rectilíneos constituyen un tipo particular de
movimientos cuyo estudio presenta un especial interés. En primer lugar, son los
movimientos más sencillos, de modo que su comprensión permite una generalización
posterior a situaciones más complejas. Estos movimientos más complicados pueden
ser estudiados como la composición de movimientos rectilíneos elementales. Tal
es el caso, por ejemplo, de los movimientos de proyectiles.
La trayectoria parabólica de una piedra que es lanzada desde un acantilado, apuntando en dirección horizontal, resulta de la composición de un movimiento rectilíneo horizontal debido al impulso recibido en el momento de lanzamiento y un movimiento rectilíneo vertical por el efecto aislado de la fuerza peso.
En segundo lugar, una buena parte de las conclusiones que se obtienen al estudiar los movimientos rectilíneos pueden extenderse a los movimientos curvilíneos si se prescinde de lo relativo a los cambios de dirección. Finalmente, estos movimientos, aunque son simples, se ajustan dentro de una buena aproximación a bastantes movimientos que se dan en la naturaleza.
Movimiento rectilíneo y uniforme
El movimiento rectilíneo y uniforme fue definido, por primera vez, por Galileo en los siguientes términos: «Por movimiento igual o uniforme entiendo aquél en el que los espacios recorridos por un móvil en tiempos iguales, tómense como se tomen, resultan iguales entre sí», o dicho de otro modo, es un movimiento de velocidad v constante.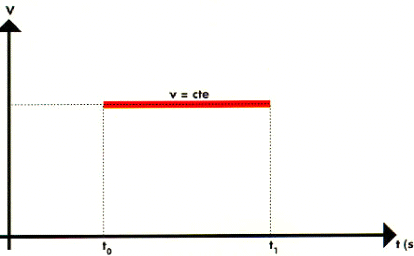
El movimiento
rectilíneo uniforme de un cuerpo, se caracteriza porque el espacio
recorrido por el móvil es directamente proporcional al tiempo
empleado, es decir, la velocidad es constante.
![]()
(1.11)
![]()
(1.12)
![]()
(1.13)
![]()
(1.14)
s = so + v · t
(1.15)
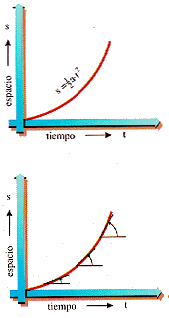
Una gráfica s-t en forma
de parábola corresponde a un movimiento uniformemente acelerado, su
pendien, que es velocidad, aumenta de un modo uniforme.
Base x altura = 30 s x 10 m/s = 300 m
Aun cuando en este caso el área no esté expresada en m2, su valor coincide numéricamente con el espacio total recorrido por el móvil durante esos 30 s:s = v · t = 30 · 10 = 300 m
A partir del diagrama v-t es posible calcular el espacio recorrido utilizando procedimientos gráficos, es decir, midiendo el área contenida bajo la gráfica. Esta propiedad no es exclusiva de este tipo de movimientos y su aplicación puede ser generalizada a otros, cualquiera que sea la forma de su gráfica v-t.

 © ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación -
www.asocae.org - RNA 592727 - CIF.: G70195805 ¦
Quiénes somos ¦
Contacto ¦
Bibliografía ¦
Política de privacidad ¦
Esta web NO utiliza cookies, ni guarda datos personales de los usuarios
© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación -
www.asocae.org - RNA 592727 - CIF.: G70195805 ¦
Quiénes somos ¦
Contacto ¦
Bibliografía ¦
Política de privacidad ¦
Esta web NO utiliza cookies, ni guarda datos personales de los usuarios




