/natureduca/fisica-ciencias-fisicas-y-medida-magnitudes-02

---

1 2

Tipos de magnitudes

ntre las distintas propiedades medibles puede establecerse una clasificación básica. Un grupo importante de ellas quedan perfectamente determinadas cuando se expresa su cantidad mediante un número seguido de la unidad correspondiente. Este tipo de magnitudes reciben el nombre de magnitudes escalares. La longitud, el volumen, la masa, la temperatura, la energía, son sólo algunos ejemplos.

Sin embargo, existen otras que precisan para su total definición que se especifique, además de los elementos anteriores, una dirección o una recta de acción y un sentido: son las llamadas magnitudes vectoriales o dirigidas. La fuerza es un ejemplo claro de magnitud vectorial, pues sus efectos al actuar sobre un cuerpo dependerán no sólo de su cantidad, sino también de la línea a lo largo de la cual se ejerza su acción.

El tiempo es una magnitud física de tipo escalar, es decir, que no depende ni de la dirección ni del sentido

Al igual que los números reales son utilizados para representar cantidades escalares, las cantidades vectoriales requieren el empleo de otros elementos matemáticos diferentes de los números, con mayor capacidad de descripción. Estos elementos matemáticos que pueden representar intensidad, dirección y sentido se denominan vectores.

Las magnitudes que se manejan en la vida diaria son, por lo general, escalares. El dependiente de una tienda de ultramarinos, el comerciante o incluso el contable, manejan masas, precios, volúmenes, etc., y por ello les es suficiente saber operar bien con números. Sin embargo, el físico, y en la medida correspondiente el estudiante de física, al tener que manejar magnitudes vectoriales, ha de operar, además, con vectores.

Algunas operaciones con vectores

La suma de dos vectores a y b con un origen común 0se define mediante la llamada regla del paralelogramo, según la cual el vector suma s es igual a la diagonal del paralelogramo -considerada como segmento orientado- formado por a, b y sus respectivas paralelas trazadas por los extremos de ambos vectores. Una de las características de la suma vectorial es que el módulo o longitud del vector suma no es igual, en general, a la suma de los módulos de los vectores sumando.

Como sucede con los números, la diferencia de dos vectores debe entenderse como la suma de uno de ellos con el opuesto del otro:

d = a - b = a + (-b)

Dado un vector v se define el opuesto de v como otro vector de igual módulo y dirección, pero de sentido contrario. Se representa como -v. Utilizando el anterior esquema del paralelogramo, el vector diferencia coincide en longitud y dirección con la otra diagonal del paralelogramo y su sentido es tal que apunta hacia el vector minuendo o primer término de la suma.

El producto de un número entero n por un vector v se define a partir de la suma en la forma:

es decir, como n veces el vector inicial. Este procedimiento se puede extender a cualquier otro número real, de modo que el producto de un vector por un número es otro vector que tiene por módulo el producto del número por el módulo del vector original, por dirección la misma y por sentido el mismo o el opuesto según el número n en cuestión sea positivo o negativo.

Suma y resta de vectores

En la suma de los vectores a + b, su vector suma Ses igual a la diagonal del paralelogramo formado por ay by sus paralelas trazadas por los extremos de ambos vectores.

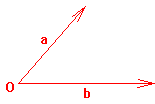
La diferencia o resta de dos vectores consiste en la suma de uno de ellos con el opuesto del otro. El opuesto del vector b es otro vector de igual módulo y dirección, pero de sentido contrario [-b]. La suma de a y -b es igual a d = a - b.

Producto de un número entero positivo o negativo por un vector V

El producto de un vector por un número es otro vector que tiene por módulo el producto del número por el módulo del vector original, por dirección la misma y por sentido el mismo o el opuesto según si el número es positivo o negativo.

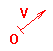
• Ejemplo de un entero positivo por un vector V:  5.V = V+V+V+V+V
• Ejemplo de un entero negativo por un vector V:  -3.V = [-V]+[-V]+[-V]

1 2

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦  Quiénes somos  ¦  Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios